今回はモンティ・ホールをエクセルを使って検証してみたいと思います。
モンティ・ホール問題とは?
モンティ・ホール問題とは以下の様な問題です。
(ウィキペディアを分かりやすい様にアレンジしています。)
■ゲームのルール
①3つのドア(1,2,3)に当たりが1つだけランダムで入っている
②あなたは必ず最初に1番のドアを選択する
③そのあと、司会者が残りのドアのうち1つを開ける
④③で司会者が開けるドアは、必ずハズレのドアである
⑤司会者はあなたにドアを選び直してもよいと言う
Q:あなたは最初に選択した1番のドアから、残りのドアに選び直しますか?
というのがモンティ・ホール問題です。
モンティ・ホール問題の当たり確率を計算
表を使うと直感でも確率が分かり易くなります。モンティ・ホール問題で起こりうるパターンは以下のA・B・Cの3パターンとなります。(○=当たり ×=ハズレ)
|
ドア番号⇒
|
1
|
2
|
3
|
|
パターンA
|
○
|
×
|
×
|
|
パターンB
|
×
|
○
|
×
|
|
パターンC
|
×
|
×
|
○
|
最初の選択(1番のドア)で当たりを引ける確率は、パターンA・B・CのうちパターンAのみですので、1/3(33.3%)となります。
一方、残りのドアに選び直した場合、当たりを引ける確率は、パターンA・B・CのうちパターンB・Cの2つですので、2/3(66.7%)となります。
よって残りのドアに選び直した方が当選しやすい(期待値が高い)事が分かります。
エクセルで大数の法則を検証する
それではエクセルで大数の法則を検証してみたいと思います。
最初の選択は1番のドアで固定して、当たりドア番号はエクセルのランダム関数を使って1~3をランダムに選択します。エクセルのセルに”=INT(RAND()*3)+1“と入力すると、1~3の整数をランダムに発生させることが出来ます。
コインを投げて、表が出る確率をグラフにします。(試行回数500回)
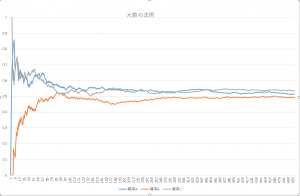
試行回数が200回を超えたあたりから、確率が理論値付近で収束している事が分かります。
試行回数200回未満の場合とくに100回未満の場合の確率というのは理論確率から遠く離れている事が分かります。
このように、試行回数が多くなればなるほど理論確率に収束していく事を大数の法則と呼びます。
扉を選び直すべきなのか?
試行回数が少ない内の結果というのは偶然(運)で支配されています。ですのでモンティ・ホール問題に何回チャレンジ出来るかが肝になってきます。
200回以上チャレンジ出来るのであれば、扉を選び直すべきなのは明らかなのですが、問題なのは試行回数が少ない場合、例えば1回しかチャレンジできないような場合、扉を選び直すべきか?というのが難しいところです。
システムトレーダーとしては、たとえ試行回数が少なくて運の要素が強く支配していたとしても、期待値の高い方を選択するべきであると思います。つまり扉を選び直すべきだと思います。
たとえ扉を選び直して外れてしまったとしても(表のパターンAで選び直してしまった場合)、それは結果論なので気にする必要は無く、常に期待値の高い方を選択するという習慣を身につける事の方が遥かに重要だと思います。