モンティ・ホール問題とは?
モンティ・ホール問題の当たり確率を計算
|
ドア番号⇒
|
1
|
2
|
3
|
|
パターンA
|
○
|
×
|
×
|
|
パターンB
|
×
|
○
|
×
|
|
パターンC
|
×
|
×
|
○
|
エクセルで大数の法則を検証する
コインを投げて、表が出る確率をグラフにします。(試行回数500回)
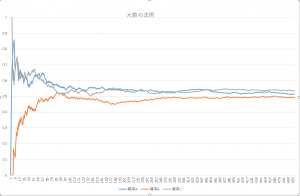
試行回数200回未満の場合とくに100回未満の場合の確率というのは理論確率から遠く離れている事が分かります。
扉を選び直すべきなのか?
偶然の無い世界
偶然の無い世界
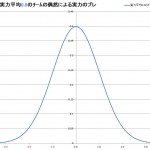
偶然による実力のブレ
実力平均0.0チームの偶然による実力のブレ
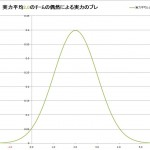
実力平均2.0チームの偶然による実力のブレ
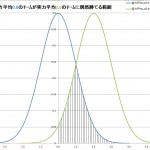
実力0.0のチームが実力2.0のチームに偶然勝てる範囲
実力0.0のチームが実力6.0のチームに偶然勝てる範囲
偶然の恩恵まとめ
体感価値や確率を定量化するプロスペクト理論
プロスペクト理論の重要な概念2つ
-
価値関数
-
確率加重関数
価値関数
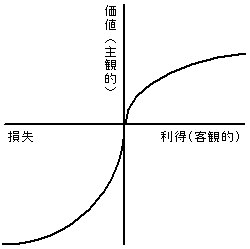
価値関数の計算式
確率加重関数
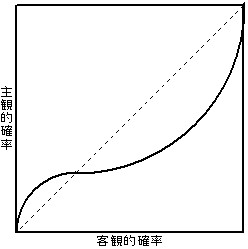
確率加重関数の計算式
プロスペクト理論から導かれる答え
おまけ:心理テスト
宝くじを買いに行く途中で交通事故にあう確率
2015年度年末ジャンボ宝くじの当選確率と還元率
|
等級
|
当選金
|
本数(1ユニット)
|
合計当選金額
|
|
1等
|
700,000千円
|
1本
|
700,000千円
|
|
1等前後賞
|
150,000千円
|
2本
|
300,000千円
|
|
1等組違い賞
|
100千円
|
199本
|
19,900千円
|
|
2等
|
10,000千円
|
20本
|
200,000千円
|
|
3等
|
1,000千円
|
200本
|
200,000千円
|
|
4等
|
50千円
|
2,000本
|
100,000千円
|
|
5等
|
3千円
|
200,000本
|
600,000千円
|
|
6等
|
0.3千円
|
2,000,000本
|
600,000千円
|
|
70周年記念賞
|
700千円
|
400本
|
280,000千円
|
|
–
|
–
|
合計⇒
|
2,999,900千円
|
宝くじを買うべきか?
交通事故にあう確率
|
平成
|
全国人口
|
交通事故数
|
確率
|
|
H26年
|
127,083千人
|
573,842件
|
1/221
|
|
H25年
|
127,298千人
|
629,033件
|
1/202
|
|
H24年
|
127,515千人
|
665,157件
|
1/192
|
|
H23年
|
127,799千人
|
692,084件
|
1/185
|
|
H22年
|
128,057千人
|
725,924件
|
1/176
|
|
–
|
–
|
平均⇒
|
1/195
|
おまけ:犯罪に巻き込まれる確率
|
平成
|
全国人口
|
刑法犯(認知件数)
|
確率
|
|
H26年
|
127,083千人
|
1,212,163件
|
1/105
|
|
H25年
|
127,298千人
|
1,314,140件
|
1/97
|
|
H24年
|
127,515千人
|
1,403,270件
|
1/91
|
|
H23年
|
127,799千人
|
1,502,802件
|
1/85
|
|
H22年
|
128,057千人
|
1,604,205件
|
1/80
|
|
–
|
–
|
平均⇒
|
1/91
|
Lotは固定した方が良い理由その3(ラスト)
-
Lot変化① = トレード結果が負けだった場合、次トレードはLotを2倍にする。
-
Lot変化② = トレード結果が勝ちだった場合、次トレードはLotを2倍にする。
-
Lot変化③:負ける度に次トレードのLotを初期Lot分増やす
-
Lot変化④:勝つ度に次トレードのLotを初期Lot分増やす
|
検証パターン
|
勝った場合
|
負けた場合
|
|
Lot可変①
|
-1枚
|
+1枚
|
|
Lot可変②
|
+1枚
|
-1枚
|
|
Lot可変③
|
-2枚
|
+1枚
|
|
Lot可変④
|
+1枚
|
-2枚
|
|
Lot可変⑤
|
-1枚
|
+2枚
|
|
Lot可変⑥
|
+2枚
|
-1枚
|
Lot固定(勝率50%、PF1のシステム)の期待値分布
Lot固定(18万通貨)の期待値分布 ※勝率50%、PF1、スプレッド0
Lot固定(17万通貨)の期待値分布 ※勝率50%、PF1、スプレッド0
Lot可変①の期待値分布(勝ったら-1枚、負けたら+1枚)
Lot可変②の期待値分布(勝ったら+1枚、負けたら-1枚)
Lot可変③の期待値分布(勝ったら-2枚、負けたら+1枚)
Lot可変④の期待値分布(勝ったら+1枚、負けたら-2枚)
Lot可変⑤の期待値分布(勝ったら-1枚、負けたら+2枚)
※縦軸=該当システム数 横軸=金額(円)
Lot可変⑥の期待値分布(勝ったら+2枚、負けたら-1枚)
まとめ
Lotは固定した方が良い理由その2
-
Lot変化③:負ける度に次トレードのLotを初期Lot分増やす
-
Lot変化④:勝つ度に次トレードのLotを初期Lot分増やす
Lot固定(勝率50%、PF1のシステム)の期待値分布
Lot固定(16万通貨)の期待値分布 ※勝率50%、PF1、スプレッド0
Lot変化③の場合の期待値分布(負ける度にロットを増やす)
Lot変化④の場合の期待値分布(勝つ度にロットを増やす)
まとめ
Lotは固定した方が良い理由
今回はLotを固定させた方が良い理由について解説させて頂きます。偶然起こったトレード結果に対してLot数を変化させる事の無意味さを検証してみたいと思います。まず今回の記事ではは以下の2点について検証してみたいと思います。
-
Lot変化① = トレード結果が負けだった場合、次トレードはLotを2倍にする。
-
Lot変化② = トレード結果が勝ちだった場合、次トレードはLotを2倍にする。
Lot固定(勝率50%、PF(プロフィットファクター)1のシステム)の期待値分布
Lot固定(15万通貨)の期待値分布 ※勝率50%、PF(プロフィットファクター)1、スプレッド0
Lot変化①の場合の期待値分布(負けたら次ロットは2倍)
Lot変化②の場合の期待値分布(勝ったら次ロットは2倍)
Lot固定とLot変化①・②の比較
まとめ
勝率とレシオの関係(±0に必要な勝率とレシオ)
1. リスクリワードレシオの基本
リスクリワードレシオ(以下、レシオ)とは 平均利益 ÷ 平均損失 で求められる数字です。例えば平均利益100pipsで平均損失100pipsのシステムであればレシオは1.0となります。
同様に平均利益200pipsで平均損失100pipsのシステムであればレシオは2.0となります。つまりレシオの数値が大きいと損小利大のシステム(手法)であり、レシオの数値が小さいと損大利小のシステム(手法)であるといえます。
2. ±0に必要な勝率を求める
±0に必要な勝率は以下の計算式で求めることが出来ます:
±0に必要な勝率 = 1 ÷ (1 + レシオ)
例えば、レシオが0.5の場合:
±0に必要な勝率 = 1 ÷ (1 + 0.5) ≒ 67%
以下に±0に必要な勝率の一覧を示します:
| リスクリワードレシオ | ±0に必要な勝率 |
|---|---|
| 2.0 | 33% |
| 1.0 | 50% |
| 0.5 | 67% |
3. ±0に必要なレシオを求める
±0に必要なレシオは以下の計算式で求めることができます:
±0に必要なレシオ = (1 – 勝率) ÷ 勝率
例えば、勝率が60%の場合:
±0に必要なレシオ = (1 – 60%) ÷ 60% ≒ 0.7
以下に±0に必要なレシオの一覧を示します:
| 勝率 | ±0に必要なリスクリワードレシオ |
|---|---|
| 30% | 2.3 |
| 40% | 1.5 |
| 50% | 1.0 |
| 60% | 0.7 |
| 70% | 0.4 |
4. レシオと勝率のどちらを軸にするべきか
システムの優位性あるいは、手法の優位性を検証する際にレシオと勝率のどちらを軸にするべきかという問題が発生します。
私は勝率を軸にして確認した方が良いと思います。理由は以下の2つです:
- 勝率は取引回数が増えれば収束するから
- 相場のボラティリティーは日々変化しているから
1つ目の理由は、勝率は取引回数が増えれば増えるほど収束していきますので基準にしやすいという点です。大ざっぱに確認する場合でも取引回数が1000回程度あれば勝率はあらかた収束したと想定する事ができます。
2つ目の理由は、相場のボラティリティーは日々変化している為、一律に損切りを100pips、利確を100pipsと固定しても結局は±0の理論確率を超えることはできないと思うからです。相場のボラティリティーに合わせて損切りや利確の値幅を変化させる必要があります。
以上の2点の理由から私は勝率を軸にして±0に必要となるレシオを確認した方が良いと判断しています。
5. まとめ
レシオと勝率どちらを軸にするにしても、利益を出すには『レシオに対する±0に必要な勝率』あるいは『勝率に対する±0に必要なレシオ』を超えなければいけません。
ランダムトレードでは期待値はスプレッド分のマイナスに収束しますので、利益を出すにはランダムトレードでは出来ない何かをする必要があります。それは待つ事です。
- 統計的優位性のあるエントリーポイントまで待つ
- 統計的優位性のあるクローズポイント(決済)まで待つ
結局のところ、この2つが利益を出す為の全てです。統計的優位性があるかどうかはシステムあるいは手法を検証する際、取引回数が1000回以上あり勝率に対する±0に必要なレシオを超えていれば優位性があると判断する事が出来るでしょう。
| EA名 | 取引回数 | 勝率 | レシオ | ±0レシオ | 差異 |
|---|---|---|---|---|---|
| リバ取り君 | 1432回 | 67% | 0.7 | 0.5 | +0.2 (133%) |
| 伸ばす君 | 2556回 | 28% | 3.2 | 2.6 | +0.7 (125%) |
※Lot0.1で2005.2.1~2015.2.1をバックテストした結果
リバ取り君の勝率67%で±0に必要なレシオは0.5です。バックテストの結果0.7という数値を出していますので、エントリーとクローズポイントに優位性があると判断できます。
同様に伸ばす君の勝率28%で±0に必要なレシオは2.6です。バックテストの結果3.2という数値を出していますのでこちらも優位性があると判断できます。
運がいい人の期待値分布
期待値0円ゲームの期待値分布検証
1. ゲームのルール
期待値0円のゲームを1000人で実施し、勝った人(0円以上)のみ次のゲームに参加します。このゲームを4回繰り返し、運がいい人の期待値分布がどのようになるのかを確認します。
ルール概要:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
| ゲーム名 | 参加条件 |
|---|---|
| テスト1 | 1000人でゲームスタート |
| テスト2 | テスト1で0円以上の利益を出した人のみ参加 |
| テスト3 | テスト2で0円以上の利益を出した人のみ参加 |
| テスト4 | テスト3で0円以上の利益を出した人のみ参加 |
| テスト5 | テスト4で0円以上の利益を出した人のみ参加 |
2. テスト1の期待値分布
テスト1の期待値分布は以下の通りです。試行回数10回を1000人が実施した際の1人当たりの期待値分布です。
条件:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
Lot=15万通貨(固定)、期待値max=+15万、期待値min=-15万、期待値平均=-960円
3. テスト2の期待値分布
テスト1で運が良かった人(624人)のみを集めて再度ゲームを行った結果の期待値分布です。
条件:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
Lot=15万通貨(固定)、期待値max=+15万、期待値min=-15万、期待値平均=-1797円
4. テスト3の期待値分布
テスト2で運が良かった人(396人)のみを集めて再度ゲームを行った結果の期待値分布です。
条件:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
Lot=15万通貨(固定)、期待値max=+12万、期待値min=-12万、期待値平均=-606円
5. テスト1~5の期待値分布比較
テスト1からテスト5まで、運が良かった人だけを集めてゲームを続けた結果、期待値分布に変化は見られませんでした。運の要素からは逃れることができないという事実が確認できました。
6. まとめ
今回の検証で以下のことが分かりました:
- 過去運が良かったからといって将来も運が良いとは限らない。
- 運は人間にコントロールできない。
「人事を尽くして天命を待つ」という言葉が示すように、運という要素が人間にコントロールできないからこそ、投資は難しくもあり、また面白いのです。
分散とヘッジ
分散とヘッジ: 相場の世界で信じられる数少ない用語
1. 分散とヘッジとは
相場の世界では、多くの専門用語が飛び交っていますが、その中には学んでも実践的な意味を持たないものもあります。例えば、ボリバン、MACD、RSIなどです。しかし、数少ない信じるに足る用語として「分散」と「ヘッジ」が挙げられます。
2. 分散 (リスク分散)
分散とはリスク分散を指します。リスク分散効果は、相関のないシステムを組み合わせてポートフォリオを構築することで得られる「フリーランチ」のようなものです。同じリスク額でも、リターンが異なるウェイト(組み込み比率)が存在することがこの理論を裏付けています。
例えば、複数の業者で取引を分散させることで、約定能力やスプレッドの違いから生じるリスクを軽減することが可能です。
3. ヘッジ (リスクヘッジ)
ヘッジとは、価格変動リスクを抑えるための手法を指します。例えば、FX取引における両建てがこれに該当します。同じタイミングで同じ枚数を両建てすれば、価格変動リスクはゼロになりますが、期待値はスプレッド分だけマイナスとなります。
金融機関のプロトレーダーであれば、リスクヘッジをせずにポジションを持つことは通常あり得ません。市場は概ね効率的であり、将来の価格変動を正確に予測することは不可能だからです。
4. システム相関の簡易分析
ポートフォリオを組む際、本来は相関係数を使った詳細な分析が求められますが、これは手間がかかります。そのため、より簡単な方法として「システムの勝率」と「取引回数」に着目する方法があります。
取引回数が多くなればなるほど、システム本来の勝率に収束していきます。この特性を利用することで、異なるロジックを持つシステムを大まかに判断することが可能です。例えば、取引回数が1000回以上あり、勝率に大きな差がある場合、それぞれのシステムは異なるロジックに基づいていると推測できます。
5. まとめ
分散とヘッジは、相場の世界で信頼できる数少ない用語です。これらを活用することで、リスクを軽減し、より安定した取引を目指すことが可能となります。特に、リスクを分散させることで、複数のシステムや業者を活用する意義が強調されます。
分散することには意義があります。複数の要素を組み合わせてリスクを軽減し、より効果的なトレードを目指しましょう。