今回はモンティ・ホールをエクセルを使って検証してみたいと思います。
モンティ・ホール問題とは?
モンティ・ホール問題とは以下の様な問題です。
(ウィキペディアを分かりやすい様にアレンジしています。)
■ゲームのルール
①3つのドア(1,2,3)に当たりが1つだけランダムで入っている
②あなたは必ず最初に1番のドアを選択する
③そのあと、司会者が残りのドアのうち1つを開ける
④③で司会者が開けるドアは、必ずハズレのドアである
⑤司会者はあなたにドアを選び直してもよいと言う
Q:あなたは最初に選択した1番のドアから、残りのドアに選び直しますか?
というのがモンティ・ホール問題です。
モンティ・ホール問題の当たり確率を計算
表を使うと直感でも確率が分かり易くなります。モンティ・ホール問題で起こりうるパターンは以下のA・B・Cの3パターンとなります。(○=当たり ×=ハズレ)
|
ドア番号⇒
|
1
|
2
|
3
|
|
パターンA
|
○
|
×
|
×
|
|
パターンB
|
×
|
○
|
×
|
|
パターンC
|
×
|
×
|
○
|
最初の選択(1番のドア)で当たりを引ける確率は、パターンA・B・CのうちパターンAのみですので、1/3(33.3%)となります。
一方、残りのドアに選び直した場合、当たりを引ける確率は、パターンA・B・CのうちパターンB・Cの2つですので、2/3(66.7%)となります。
よって残りのドアに選び直した方が当選しやすい(期待値が高い)事が分かります。
エクセルで大数の法則を検証する
それではエクセルで大数の法則を検証してみたいと思います。
最初の選択は1番のドアで固定して、当たりドア番号はエクセルのランダム関数を使って1~3をランダムに選択します。エクセルのセルに”=INT(RAND()*3)+1“と入力すると、1~3の整数をランダムに発生させることが出来ます。
コインを投げて、表が出る確率をグラフにします。(試行回数500回)
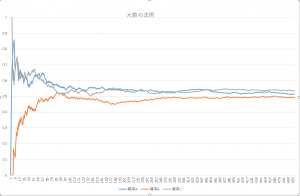
試行回数が200回を超えたあたりから、確率が理論値付近で収束している事が分かります。
試行回数200回未満の場合とくに100回未満の場合の確率というのは理論確率から遠く離れている事が分かります。
このように、試行回数が多くなればなるほど理論確率に収束していく事を大数の法則と呼びます。
扉を選び直すべきなのか?
試行回数が少ない内の結果というのは偶然(運)で支配されています。ですのでモンティ・ホール問題に何回チャレンジ出来るかが肝になってきます。
200回以上チャレンジ出来るのであれば、扉を選び直すべきなのは明らかなのですが、問題なのは試行回数が少ない場合、例えば1回しかチャレンジできないような場合、扉を選び直すべきか?というのが難しいところです。
システムトレーダーとしては、たとえ試行回数が少なくて運の要素が強く支配していたとしても、期待値の高い方を選択するべきであると思います。つまり扉を選び直すべきだと思います。
たとえ扉を選び直して外れてしまったとしても(表のパターンAで選び直してしまった場合)、それは結果論なので気にする必要は無く、常に期待値の高い方を選択するという習慣を身につける事の方が遥かに重要だと思います。
偶然の無い世界
今回は偶然の無い世界について考えてみたいと思います。
この世は偶然の出来事に満ち満ちています。自分の方が実力が上なのに運が悪ければ、自分より実力が下の人に敗れる事も多々あります。とても不条理で不合理な世界です。
ではこの世から偶然という概念が無くなったらどうなるのでしょうか?
偶然の要素が無くなった世界を想像してみたいと思います。
偶然の無い世界
実力のある人は必ず実力の劣る人に勝つ世界。逆にいえば実力の劣る人は絶対に実力のある人に勝てない世界。
どうでしょうか。偶然の無い世界は、とても退屈な世界だと私は思いました。
偶然の出来事があるからこそ、人々はそれに希望を抱き、希望を糧にして目標に向かって努力出来るのです。あるいは偶然起こった奇跡を皆で喜びそれを共有する事が出来るのです。
偶然の無い世界というのは希望を抱く事の出来ない何の面白味も無い世界だと私は思います。
偶然による実力のブレ
では具体的に偶然による実力のブレを見てみたいと思います。想像しやすい様に各実力をスポーツ戦における各チームの実力と想定してみて下さい。
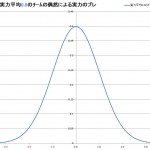
実力平均0.0チームの偶然による実力のブレ
こちらが実力0.0のチームが偶然によって起こりうる実力のブレとなっています。
(平均0.0 標準偏差1 の正規分布)
実力は0.0ですが、運が悪ければ-4.0しか力が出せない事もあるし、逆に運が良ければ+4.0という力を出す事ができます。
この-4.0~+4.0の違いは何なのでしょうか?これがまさに偶然(運)なのです。
つまり実力は0.0なのですが、偶然の要素によってのこチームの実力は-4.0~+4.0の間にあると言えます。偶然の要素とはチームの士気であったり、選手の体調がこれにあたるでしょう。
この偶然(運)があるからこそ決着がつくともいえます。もし偶然(運)が無い場合、実力が0.0同士のチームが戦った場合永遠に決着がつかない事になります。
では次に実力平均2.0のチームの偶然による実力のブレを見てみたいと思います。
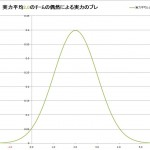
実力平均2.0チームの偶然による実力のブレ
こちらが実力2.0のチームが偶然によって起こりうる実力のブレとなっています。
(平均2.0 標準偏差1 の正規分布)
実力は2.0ですが、運が悪ければ-2.0しか力が出せない事もあるし、逆に運が良ければ+6.0という力を出すことが出来るというのが分かります。
では実力0.0のチームと実力2.0のチームが試合をした場合どうなるか見てみましょう。
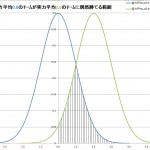
実力0.0のチームが実力2.0のチームに偶然勝てる範囲
縦線がひいてある範囲が、実力0.0のチームが実力2.0のチームに偶然勝てる範囲となっています。
つまりこの範囲においては、どちらのチームが勝つか分からない実力の拮抗した状態という事になります。
通常、野球でもサッカーでもバレーでも勝負事において白熱するのはこのような実力が拮抗した状態であり、観客はこれを見たいが為に現地に足を運んでいるわけです。
チームの実力が違うのにこのようにどちらが勝つか分からない拮抗した状態になるのは、偶然という概念がある事の恩恵そのものです。
もし偶然という概念がなければ実力2.0のチームが必ず勝つ試合になるわけですから、面白味の全くない試合であり、誰も結果が分かっている試合を見たいとは思わないはずです。
それでは最後に奇跡という偶然を確認してみましょう
実力0.0のチームが実力6.0のチームに偶然勝てる範囲
縦線がひいてある範囲が、実力0.0のチームが実力6.0のチームに偶然勝てる範囲となっています。
まさに奇跡的な確率ではありますが、実力0.0のチームが実力6.0のチームに勝てる可能性があります。このようにお互いの実力が離れれば離れるほど偶然勝てる範囲も狭くなってきます。
おそらくこの試合を見ている人のほとんどが実力6.0のチームが勝つであろうと思って試合を観戦しているはずです。
例えば実力0.0のチームを高校生野球チーム、実力6.0のチームをプロ野球チームと置き換えると分かり易いかと思います。
誰も高校生野球チームが勝てるとは思っていないわけです。しかし、偶然が起こりうる確率が低ければ低い程それが実現した時の感動というのは大きくなります。つまり高校生野球チームが奇跡的に勝った場合、観客が大いに盛り上がる事が想像できます。
偶然の恩恵まとめ
偶然というのは時には不条理かつ不合理な側面もありますが、この様に人々に感動や喜びを与える上で非常に重要な概念である事が分かりました。
システムトレードにおいても同様で、システム本来の実力以上に運よく偶然勝つ事もあれば、運悪く偶然負けることもあります。
偶然というのは避けることの出来ない普遍的な事だということを理解したうえで、もし偶然運よく実力以上に勝てた場合は大いに喜べば宜しいかと思います。
逆に運悪く実力以上に負けた場合、悲しむ必要はありません。偶然負けただけなのですから気にしてもしょうがないです。切り替えていきましょう。
偶然という普遍的な概念を理解したうえで、自分の都合の良い方に解釈すればいいということになります。ポジティブシンキングで行きましょう。
体感価値や確率を定量化するプロスペクト理論
今回はプロスペクト理論について解説させて頂きます。プロスペクト理論を一言でいうと人間が感じる価値や確率(体感価値・確率)を定量的に表現するために使う理論です。
プロスペクト理論はカーネマン博士によってノーベル経済学賞を受賞されております。
プロスペクト理論の重要な概念2つ
-
価値関数
-
確率加重関数
プロスペクト理論には価値関数と確率加重関数という2つの重要な概念があります。難しそうな言葉ですが、内容はいたって簡単です。百聞は一見にしかずという事で早速下記グラフをご覧ください。
価値関数
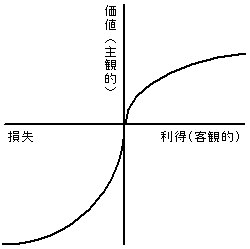
こちらのグラフが価値関数というグラフで、価値について人間が感じる体感価値と実際の価値との関係を表したものです。
横軸が客観的価値(実際の価値)を表しており、縦軸が主観的価値(体感価値)を表しております。
客観的価値(実際の価値)が+1.0の場合の主観的価値(体感価値)は+1.0という事が分かりますが、客観的価値(実際の価値)が-1.0の場合の主観的価値(体感価値)は-2.25となっています。
この主観的価値(体感価値)の不均衡が何を意味しているのかと言うと、人間は得したときの体感よりも、損をしたときの心理的(体感的)ダメージの方が大きいという事が定量的に表わされています。
つまり、客観的には±1.0の価値でも、体感ではプラスの場合は+1.0ですがマイナスの場合は-2.25というプラスの場合の2.25倍の心理的(体感的)ダメージがあるという事です。
例えば、100万円利益を出したあとに100万円損しても実収支は±0円なのですが、心理的(体感的)には-125万円損した気分だという事です。(100万×1倍 + -100万×2.25倍 = -125万)
価値関数の計算式
出所⇒wiki
上記グラフでは α=0.88、β=0.88、λ=2.25 の推定値を使用
出所⇒Kahneman and Tversky(1992) のレポートの311p参照
確率加重関数
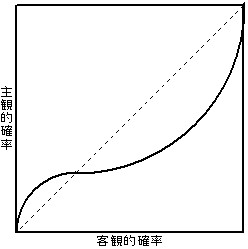
こちらのグラフが確率加重関数というグラフで、確率について人間が感じる体感確率と実際の確率をの関係を表したものです。
横軸が客観的確率(実際の確率)を表しており、縦軸が主観的確率(体感確率)を表しております。
赤い点線が本来の確率です。ここで注目して頂きたいのが、青い矢印の部分と黄色い矢印の部分です。
青い矢印の部分は本来の確率よりも体感的に過大評価してしまう部分で、逆に黄色い矢印の部分は本来の確率より体感的に過小評価してしまう部分です。
つまり、確率が低い場合人間は体感的に過大評価する傾向にあり、確率が高い場合人間は体感的に過小評価してしまうということです。
例えば、宝くじに当選する事(当選確率1/2000万)には期待するが(過大評価)、交通事故にあう(交通事故確率=1/195)なんて考えていない(過小評価)といった感じです。
確率加重関数の計算式
出所⇒wiki
上記グラフでは γ=0.61、δ=0.69 の推定値を使用
出所⇒Kahneman and Tversky(1992) のレポートの312p参照
プロスペクト理論から導かれる答え
一つ目のグラフ(価値関数)も二つ目のグラフ(確率加重関数)も共に、客観的価値・確率(実際の価値・確率)と主観的価値・確率(体感価値・確率)の関係を表したものです。
この体感価値・確率(心理)という漠然としたものを定量的に表す事ができる点でプロスペクト理論というのは非常に面白いと思います。流石ノーベル経済学賞を受賞された理論だけの事はあります。
価値関数によって、価値に関して人間は利益より損失を苦痛と感じるという事が分かりました。これは損失を苦痛と感じるがゆえに損切り出来ずに損大利小のトレードになってしまう心理、又は利益がでるとすぐに利確してしまう心理を証明しています。
確率加重関数によって、確率に関して人間は低確率のものを高く見積もる傾向にある事が分かりました。これは勝率30%のシステムを運用しているのに、毎回利益を期待してしまう心理の証明であります。実際勝率30%というのはほとんどが損切りです。システムを開発した自分でさえも嫌になる程に損切りばかりします。
システムトレーダーの場合、価値関数に関してはシステムが自動で売買を執行しますので特に関係ありませんが、確率加重関数の点については理解しておく必要があります。
自分の運用しているシステムの勝率がいくらで、どのぐらい連敗する可能性があるか把握していても、頭で分かっていてもいざ実際連敗するとガッカリしてしまうものです。
そういう時は私たちがシステムトレードで自動売買している理由を思い出してください。相場は自動売買に任せて、この有限で貴重な時間を相場以外に使えるというのがシステムトレーダーの最大の強みなハズです。
折角自動売買しているのに、取引の度に一喜一憂していては本末転倒です。システムが正常に稼働しているかのチェックだけしてトレード結果は無視する位が丁度いいです。
たとえ米国雇用統計が不利な方に3円飛ぼうとそれだけで一発退場するようなリスクは取っていませんから、どんと構えていきましょう。その為に統計分析してリスク管理している訳ですから。
おまけ:心理テスト
最後に、wikiをアレンジした質問をしてみたいと思います。
Q:あなたは以下の選択肢 aと b のどちらを選びますか?
・a ⇒ 100万円が無条件で手に入る。
・b ⇒ コインを投げ表が出たら300万円手に入るが、裏が出たらハズレ。
こいう問題がでたらとりあえず期待値を計算してみましょう。
aの期待値 = 100% × 100万円 = 100万円
bの期待値 = 50% × 300万円 + 50% × 0円 = 150万円
以上の事よりbの方が期待値が高い事が分かりました。では期待値が高いという理由一点のみでbを選択するべきなのでしょうか?
正解は、プレイできる回数によるです。aの場合外れるリスクはありませんが、bの場合は50%あります。つまり50%に収束するまでの試行回数をプレイできるかどうかが重要となります。
もしこのゲームに1回しか挑戦出来ないのであれば、私は迷わずにaを選択して無リスクで100万円を貰います。
1回しか挑戦出来ないのに、例えばあなたがbの方が期待値が高いからbに決まってるやん!(ドヤァ)と選択してコインが外れた場合、仕方ないと諦められますか?
価値関数によると、150万円 × 2.25 ≒ 338万円を失った心理的(体感的)ダメージを受けることになります。
むろんこのゲームに400プレイ程度挑戦できるのであれば、迷わずbを選ぶべきですが。
確率別の収束速度
つまり、期待値が高いからという1つの理由のみで判断するのは危険だということです。ゲームに参加するにはまず期待値がプラスであることは当然ですが、確率が収束するだけの試行回数プレイできるかを確認してからそのゲームに参加するか判断する必要があります。
宝くじを買いに行く途中で交通事故にあう確率
今年も年末ジャンボ宝くじの発売が開始されました。今回は宝くじの還元率と当選確率、そして宝くじを買いにいく途中で交通事故にあう確率を求めてみたいと思います。
2015年度年末ジャンボ宝くじの当選確率と還元率
宝くじの当選確率と還元率を計算するのは簡単です。みずほ銀行のHPに計算するのに必要なデータは全て公開されています。
みずほ銀行/宝くじホーム
今回は1ユニットが2000万枚となっており、1ユニットにつき1等が1本ありその当選金が7億円となっています。どうやら前後賞合わせて10億円というのが今年のキャッチフレーズの様です。
という事で1等の当選確率は1/2000万という事が分かりました。では還元率を計算してみたいと思います。まずは1ユニット当たりの合計当選金額を求めていきます。
|
等級
|
当選金
|
本数(1ユニット)
|
合計当選金額
|
|
1等
|
700,000千円
|
1本
|
700,000千円
|
|
1等前後賞
|
150,000千円
|
2本
|
300,000千円
|
|
1等組違い賞
|
100千円
|
199本
|
19,900千円
|
|
2等
|
10,000千円
|
20本
|
200,000千円
|
|
3等
|
1,000千円
|
200本
|
200,000千円
|
|
4等
|
50千円
|
2,000本
|
100,000千円
|
|
5等
|
3千円
|
200,000本
|
600,000千円
|
|
6等
|
0.3千円
|
2,000,000本
|
600,000千円
|
|
70周年記念賞
|
700千円
|
400本
|
280,000千円
|
|
–
|
–
|
合計⇒
|
2,999,900千円
|
1ユニット当たりの合計当選金額が2,999,900千円というのが分かりました。1ユニットを購入するのに必要な金額は、300円×2000万枚=6,000,000千円ですので、還元率は以下の通り求める事が出来ます。
宝くじの還元率 = 2,999,900千円 ÷ 6,000,000千円 ≒ 50%
という事で、宝くじというゲームは宝くじを購入したプレイヤー全員から集めたお金の50%を奪い合うマネーゲームであるという事を理解する必要があります。
宝くじも、れっきとしたマネーゲームなのですが、普段FXや株などのマネーゲームを毛嫌いしている人達もなぜか宝くじだけは抵抗なく購入しています。
宝くじからマネーゲームの匂いを一切排除し、夢と希望に満ち溢れた商品だと勘違いさせる高度に専門的な技術は流石の電通といった所でしょうか。
宝くじを買うべきか?
期待値がマイナスの時点で確率の収束速度を考えるまでも無く、通常のマネーゲームであればまず参加しませんが、宝くじというのは1/2000万と当選確率が非常に低い代わりにリターンが7億円と飛びぬけて高くなっています。
300円のリスクで7億円のリターンに当選する確率が0を超えている(0では無い)という点では確かに夢はあります。
期待値はマイナスですが、割り切って1枚300円分だけ買って当たったら何をしよう?と妄想して年末を楽しむのはありかもしれません。
宝くじは胴元が半分持っていく酷いビジネスモデルなのですが、人々に僅かながらの希望や夢を与えているという意味においては社会に貢献しているのかもしれません。まあ正月になれば、夢は儚く散り現実に戻されるわけですが。
交通事故にあう確率
では宝くじを買いにいく途中で交通事故にあう確率を求めてみたいと思います。1年間で交通事故にあう確率は以下のとおりです。
※確率の計算式 = 交通事故数(年) ÷ 全国人口(年)
出所:交通事故数⇒警視庁/統計、全国人口⇒総務省統計局/統計データ
|
平成
|
全国人口
|
交通事故数
|
確率
|
|
H26年
|
127,083千人
|
573,842件
|
1/221
|
|
H25年
|
127,298千人
|
629,033件
|
1/202
|
|
H24年
|
127,515千人
|
665,157件
|
1/192
|
|
H23年
|
127,799千人
|
692,084件
|
1/185
|
|
H22年
|
128,057千人
|
725,924件
|
1/176
|
|
–
|
–
|
平均⇒
|
1/195
|
1年間で交通事故にあう確率は平均1/195に対して、1年間で年末ジャンボ宝くじ1等に当選する確率は1/2000万。という事で、1等に当選するより交通事故にあう確率の方が10万倍高いという事が分かりました。
宝くじを買いに行く際はシートベルトを着用し、くれぐれも安全運転でお願いします。
おまけ:犯罪に巻き込まれる確率
最後に犯罪に巻き込まれる確率を求めてみたいと思います。1年間で犯罪に巻き込まれる確率は以下のとおりです。
※確率の計算式 = 刑法犯認知件数(年) ÷ 全国人口(年)
出所:刑法犯認知件数⇒警視庁/統計、全国人口⇒総務省統計局/統計データ
|
平成
|
全国人口
|
刑法犯(認知件数)
|
確率
|
|
H26年
|
127,083千人
|
1,212,163件
|
1/105
|
|
H25年
|
127,298千人
|
1,314,140件
|
1/97
|
|
H24年
|
127,515千人
|
1,403,270件
|
1/91
|
|
H23年
|
127,799千人
|
1,502,802件
|
1/85
|
|
H22年
|
128,057千人
|
1,604,205件
|
1/80
|
|
–
|
–
|
平均⇒
|
1/91
|
日本は世界でもトップクラスに治安がいいのですが、それでも1年間で犯罪に巻き込まれる確率は平均で1/91とけっして低い確率ではない事が分かります。犯罪に巻き込まれない様に普段から自己防衛していく事の大切さが分かります。
Lotは固定した方が良い理由その3(ラスト)
今回もトレード結果に対してLot数を変化させる事の無意味さを検証していきたいと思います。前回の記事までで以下の4パターンを検証しトレード結果に対してLotを変化させても優位性があるとはいえない事を確認しました。
-
Lot変化① = トレード結果が負けだった場合、次トレードはLotを2倍にする。
-
Lot変化② = トレード結果が勝ちだった場合、次トレードはLotを2倍にする。
Lotは固定した方が良い理由
-
Lot変化③:負ける度に次トレードのLotを初期Lot分増やす
-
Lot変化④:勝つ度に次トレードのLotを初期Lot分増やす
Lotは固定した方が良い理由その2
今回はもっと細かくLotを上下に可変させた場合どういう期待値分布になるのを検証していきたいと思います。具体的には下記6パターン(Lot可変①~⑥)をこれから検証していきます。
|
検証パターン
|
勝った場合
|
負けた場合
|
|
Lot可変①
|
-1枚
|
+1枚
|
|
Lot可変②
|
+1枚
|
-1枚
|
|
Lot可変③
|
-2枚
|
+1枚
|
|
Lot可変④
|
+1枚
|
-2枚
|
|
Lot可変⑤
|
-1枚
|
+2枚
|
|
Lot可変⑥
|
+2枚
|
-1枚
|
Lot固定(勝率50%、PF1のシステム)の期待値分布
まずLot可変①~④のベンチマークとなるLot固定(18万通貨)と、Lot可変⑤~⑥のベンチマークとなるLot固定(17万通貨)の期待値分布がこちらになります。
※試行回数10回を1000セット実施した時の1セット当たりの期待値分布
Lot固定(18万通貨)の期待値分布 ※勝率50%、PF1、スプレッド0
※縦軸=該当システム数 横軸=金額(円)
Lot固定(17万通貨)の期待値分布 ※勝率50%、PF1、スプレッド0
※縦軸=該当システム数 横軸=金額(円)
2つ共に期待値0円付近(-756円と+306円)を頂点とした正規分布になっている事が確認できます。このLot固定の分布をベンチマークとして、Lotを可変させた場合の分布と比較し、Lotを可変させる事に優位性があるのか検証していきたいと思います。
Lot可変①の期待値分布(勝ったら-1枚、負けたら+1枚)
Lot可変① = トレード結果が勝ちだった場合-1枚、負けだった場合+1枚にLotを可変させる
※初期Lotを18万通貨として、トレード結果に応じて±1枚させる。
(最小Lot=9枚、最大Lot=27枚、平均Lot=18枚)
※縦軸=該当システム数 横軸=金額(円)
赤の線がLot可変①の分布となっています。Lot固定の分布(青色)とほぼ同じ形をしていますが、マイナス側の曲線が歪んでしまっています。
期待値平均も0付近(-276円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot可変②の期待値分布(勝ったら+1枚、負けたら-1枚)
Lot可変② = トレード結果が勝ちだった場合+1枚、負けだった場合-1枚にLotを可変させる
※初期Lotを18万通貨として、トレード結果に応じて±1枚させる。
(最小Lot=9枚、最大Lot=27枚、平均Lot=18枚)
※縦軸=該当システム数 横軸=金額(円)
赤の線がLot可変②の分布となっています。Lot固定の分布(青色)とほぼ同じ形をしていますが、プラス側の曲線が歪んでしまっています。
期待値平均も0付近(+440円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot可変③の期待値分布(勝ったら-2枚、負けたら+1枚)
Lot可変③ = トレード結果が勝ちだった場合-2枚、負けだった場合+1枚にLotを可変させる
※初期Lotを20万通貨として、トレード結果に応じてLotを可変させる。
(最小Lot=2枚、最大Lot=29枚、平均Lot=18枚)
※縦軸=該当システム数 横軸=金額(円)
赤の線がLot可変③の分布となっています。Lot固定の分布(青色)と比べると、山がつぶされて平たくなり、分布の幅が広くなっていることが分かります。
Lot固定の場合よりも偶然(運)による振れ幅が大きい=リスクが大きくなってしまっているという事を表しています。期待値平均も0付近(-583円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot可変④の期待値分布(勝ったら+1枚、負けたら-2枚)
Lot可変④ = トレード結果が勝ちだった場合+1枚、負けだった場合-2枚にLotを可変させる
※初期Lotを20万通貨として、トレード結果に応じてLotを可変させる。
(最小Lot=2枚、最大Lot=29枚、平均Lot=18枚)
※縦軸=該当システム数 横軸=金額(円)
赤の線がLot可変④の分布となっています。Lot固定の分布(青色)と比べると、こちらも山がつぶれて平たくなり、分布の幅が広くなっている事が分かります。
Lot固定の場合よりもリスクが大きくなってしまっており、期待値平均も0付近(-470円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot可変⑤の期待値分布(勝ったら-1枚、負けたら+2枚)
Lot可変⑤ = トレード結果が勝ちだった場合-1枚、負けだった場合+2枚にLotを可変させる
※初期Lotを15万通貨として、トレード結果に応じてLotを可変させる。
(最小Lot=6枚、最大Lot=31枚、平均Lot=17枚)
※縦軸=該当システム数 横軸=金額(円)
赤の線がLot可変⑤の分布となっています。Lot固定の分布(青色)と比べると、こちらも山がつぶれて平たくなり、分布の幅が広くなっている事が分かります。
Lot固定の場合よりもリスクが大きくなってしまっており、期待値平均も0付近(+649円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot可変⑥の期待値分布(勝ったら+2枚、負けたら-1枚)
Lot可変⑥ = トレード結果が勝ちだった場合+2枚、負けだった場合-1枚にLotを可変させる
※初期Lotを15万通貨として、トレード結果に応じてLotを可変させる。
(最小Lot=6枚、最大Lot=31枚、平均Lot=17枚)
※縦軸=該当システム数 横軸=金額(円)
赤の線がLot可変⑥の分布となっています。Lot固定の分布(青色)と比べると、こちらも山がつぶれて平たくなり、分布の幅が広くなっている事が分かります。
Lot固定の場合よりもリスクが大きくなってしまっており、期待値平均も0付近(-565円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
まとめ
最後に乱数を変えて分布がどうなるか確認しましょう。
期待値分布(Lot固定 vs Lot変化) その3
この様に乱数を何度変えてもトレード結果に応じてLotを変化させる事に優位性があるとはいえない事が分かります。
様々なパターンを検証してきましたが、結局のところLot固定より優位性があるパターンはありませんでした。なぜこのような結果になるのでしょうか?
それはトレードの勝った負けたという結果は偶然の産物に過ぎないからです。偶然起こった結果に対してLotを変化させたところで統計的優位性は無いという事が今回証明されました。
優位性が無いだけではなく正規分布の形が左右対称では無くなり、リスク管理が難しくなってしまいます。つまりLotは固定した方がリスク管理しやすいといえるでしょう。
一言でいうと シンプル IS ベスト でしょうか。
Lotは固定した方が良い理由その2
今回もトレード結果に対してLot数を変化させる事の無意味さを検証していきたいと思います。前回記事ではLot変化①(負けたら次ロットは2倍)とLot変化②(勝ったら次ロットは2倍)の2パターンを検証しました。
Lotは固定した方が良い理由
今回は以下の2パターンを検証していきます。
-
Lot変化③:負ける度に次トレードのLotを初期Lot分増やす
-
Lot変化④:勝つ度に次トレードのLotを初期Lot分増やす
Lot固定(勝率50%、PF1のシステム)の期待値分布
まず今回のベンチマークとなる固定Lot(16万通貨)の期待値分布を確認してみたいと思います。
※試行回数10回を1000セット実施した時の1セット当たりの期待値分布
Lot固定(16万通貨)の期待値分布 ※勝率50%、PF1、スプレッド0
※縦軸=該当システム数 横軸=金額(円)
期待値0円付近(+672円)を頂点とした正規分布になっている事が確認できます。このLot固定の分布をベンチマークとして、Lotを変化させた場合の分布と比較し、Lotを変化させる事に優位性があるのか検証していきたいと思います。
Lot変化③の場合の期待値分布(負ける度にロットを増やす)
Lot変化③ = トレード結果が負けだった場合、次トレードのLotを初期Lot分増やす
※初期Lotを5万通貨として、負ける度に5万通貨ずつ増やす。
※縦軸=該当システム数 横軸=金額(円)
紫の線がLot変化③の分布となっています。Lot固定の分布(青色)と比べると、山がつぶされて平たくなり、分布の幅が広くなっていることが分かります。
Lot固定の場合よりも偶然(運)による振れ幅が大きい=リスクが大きくなってしまっているという事を表しています。期待値平均も0付近(450円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot変化④の場合の期待値分布(勝つ度にロットを増やす)
Lot変化④ = トレード結果が勝ちだった場合、次トレードのLotを初期Lot分増やす
※初期Lotを5万通貨として、勝つ度に5万通貨ずつ増やす。
※縦軸=該当システム数 横軸=金額(円)
オレンジの線がLot変化④の分布となっています。Lot固定の分布(青色)と比べると、こちらも山がつぶれて平たくなり、分布の幅が広くなっている事が分かります。
先ほどと同じく、Lot固定の場合よりもリスクが大きくなってしまっており、期待値平均も0付近(-440円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
それでは最後に乱数を変えて分布がどう変化するか確認してみましょう。
期待値分布(Lot固定 vs Lot変化) その2
何度乱数を変えても、トレード結果に応じてLotを変化させる事に優位性があるとはいえない事が分かります。
まとめ
今回の2パターンも、トレード結果に応じてLotを変化させてもLotを固定させた場合よりも優位性があるとはいえない結果となりました。次回はもっと細かくLotを上下に可変させた場合どうなるか検証したいと思います。
Lotは固定した方が良い理由
今回はLotを固定させた方が良い理由について解説させて頂きます。偶然起こったトレード結果に対してLot数を変化させる事の無意味さを検証してみたいと思います。まず今回の記事ではは以下の2点について検証してみたいと思います。
-
Lot変化① = トレード結果が負けだった場合、次トレードはLotを2倍にする。
-
Lot変化② = トレード結果が勝ちだった場合、次トレードはLotを2倍にする。
Lot変化①となる心理状態としては、負けを取り戻そうと焦る心理あるいは、負けた後は勝つ可能性が高いのではないかと期待する心理状態です。
Lot変化②となる心理状態としては、ついてる時はついてるから勝てると期待する心理あるいは、勝った分を直ぐに複利で運用したいという心理状態です。
もちろんLot変化①も②も全て感情論で何の統計的根拠もありません。そのことをこれから証明していきたいと思います。
Lot固定(勝率50%、PF(プロフィットファクター)1のシステム)の期待値分布
まずベンチマークとなるLot固定(15万通貨)の期待値分布がこちらになります。
※試行回数10回を1000セット実施した時の1セット当たりの期待値分布
Lot固定(15万通貨)の期待値分布 ※勝率50%、PF(プロフィットファクター)1、スプレッド0
※縦軸=該当システム数 横軸=金額(円)
このシステムの理論期待値は0円です。分布をみても期待値0円付近(-570円)を頂点とした正規分布になっている事が確認できます。0円未満の成績は運が悪かったと言えますし、0円超えの成績は運が良かったと言えます。
この様に運(偶然)は避けることの出来ない普遍的な事だということを理解する必要があります。
ではこの分布をベンチマークとしてLotを変化させた場合と比較していきたいと思います。
Lot変化①の場合の期待値分布(負けたら次ロットは2倍)
Lot変化① = トレード結果が負けだった場合、次トレードはLotを2倍にする。
※初期Lotを10万通貨として、負けた場合20万通貨にLotを変化させる。
※縦軸=該当システム数 横軸=金額(円)
赤い線がLot変化①の分布となっています。先ほどのLot固定の分布(青色)と比べると、山がつぶされて平たくなり、分布の幅が広くなっていることが分かります。
Lot固定の場合よりも偶然(運)による振れ幅が大きい=リスクが大きくなってしまっているという事を表しています。期待値平均も0付近(-1390円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot変化②の場合の期待値分布(勝ったら次ロットは2倍)
Lot変化② = トレード結果が勝ちだった場合、次トレードはLotを2倍にする。
※初期Lotを10万通貨として、勝った場合20万通貨にLotを変化させる。
※縦軸=該当システム数 横軸=金額(円)
緑の線がLot変化②の分布となっています。Lot固定の分布(青色)と比べると、こちらも山がつぶれて平たくなり、分布の幅が広くなっている事が分かります。
先ほどと同じく、Lot固定の場合よりもリスクが大きくなってしまっており、期待値平均も0付近(-730円)でLot固定の場合と比べても特に優位性があるとはいえない事が確認できます。
Lot固定とLot変化①・②の比較
この様にLotをトレード結果に応じて変化させたところで統計的優位性があるとは言えない事が分かりました。優位性が無いだけではなく、Lot変化させた場合は分布の形が左右非対称の山型となってしまっています。
私が統計分析する時はリスクの発生を標準正規分布で仮定して全て計算しています。標準正規分布とは平均0、標準偏差1となる下記の様な左右対称の山型グラフです。
という事でLot変化させたシステムを分析する場合、計算にズレが生じます。特に最大DDの予測などの分析結果にズレが生じてしまっては致命傷となる恐れもあります。
以上の事から、トレード結果に応じてLot数を変化させるメリットは無いと現在のところ私は思っています。
もし”勝率50%+リスクリワード1:1で利益が出せる資金管理方法”なんてタイトルがあったら、まず試行回数を確認してみて下さい。試行回数が数十回程度であればそれはただの資金管理によるカーブフィッティングである可能性が非常に高いです。
勝率50%に収束するには少なくとも400回程度の試行回数が必要です。
それでは最後に乱数を変えて分布がどのように変化するか確認してみましょう。
期待値分布(Lot固定 vs Lot変化)
何度乱数を変えても、トレード結果に応じてLotを変化させる事に優位性があるとはいえない事が分かります。
まとめ
口座を複利で運用する場合は、最低でも数月単位でLotを調整する必要があります。間違えてもトレードで利益が出たからといって直ぐに複利計算してLotを増やしてはいけません。
日々のトレードは単利で考えて、半年に一回複利になるようLot調整する位で丁度いいという事になります。
関連記事
Lotは固定した方が良い理由その2
Lotは固定した方が良い理由その3(ラスト)
勝率とレシオの関係(±0に必要な勝率とレシオ)
今回は勝率とリスクリワードレシオの関係について解説させて頂きます。
リスクリワードレシオ
リスクリワードレシオ(以下、レシオ)とは 平均利益 ÷ 平均損失 で求められる数字です。例えば平均利益100pipsで平均損失100pipsのシステムであればレシオは1.0となります。
同様に平均利益200pipsで平均損失100pipsのシステムであればレシオは2.0となります。つまりレシオの数値が大きいと損小利大のシステム(手法)であり、レシオの数値が小さいと損大利小のシステム(手法)であるといえます。
レシオを求めただけではシステム(手法)の優劣は判断できません。レシオに対して±0に必要な勝率を超えているかどうかを確認する必要があります。
例えばレシオが1.0の場合、勝率が50%で±0となります。もしレシオが1.0で勝率が50%未満であればトータルで損失を出しますし、逆に勝率50%を越えていればトータルで利益を出せます。
それではレシオに対する±0に必要な勝率を求めていきたいと思います。
±0に必要な勝率を求める(レシオが軸)
±0に必要な勝率は以下の計算式で求めることが出来ます。
±0に必要な勝率 = 1 ÷ ( 1 + レシオ )
※レシオ = 平均利益 ÷ 平均損失
この式を使ってレシオが0.5の場合、±0に必要な勝率を求めてみますと、
■±0に必要な勝率 = 1 ÷ ( 1 + 0.5 ) ≒ 67% となります。
つまりレシオ0.5で勝率が67%を超えていれば利益が出ていると言う事になります。
±0に必要な勝率一覧(レシオが軸)
以下が±0に必要な勝率の一覧となります。
|
リスクリワードレシオ
|
±0に必要な勝率
|
|
2.0
|
33%
|
|
1.0
|
50%
|
|
0.5
|
67%
|
それでは今度は、勝率を軸にして±0にするのに必要なレシオを求めてみたいと思います。
±0に必要なレシオを求める(勝率を軸)
±0に必要なレシオは冒頭の計算式を変形して以下の様に求めることができます。
±0に必要なレシオ = ( 1 - 勝率 ) ÷ 勝率
※レシオ = 平均利益 ÷ 平均損失
この式を使って勝率が60%の場合、±0に必要なレシオを求めてみますと、
■±0に必要なレシオ = ( 1 – 60% ) ÷ 60% ≒ 0.7 となります。
つまり勝率60%でレシオが0.7を超えていれば利益が出いてるという事になります。
±0に必要なレシオ一覧(勝率を軸)
以下が±0に必要なレシオの一覧となります。
|
勝率
|
±0に必要なリスクリワードレシオ
|
|
30%
|
2.3
|
|
40%
|
1.5
|
|
50%
|
1.0
|
|
60%
|
0.7
|
|
70%
|
0.4
|
レシオと勝率のどちらを軸にするべきか
システムの優位性あるいは、手法の優位性を検証する際に上記の様にレシオと勝率のどちらを軸にするべきかという問題が発生します。
私は勝率を軸にして確認した方が良いと思います。理由は以下の2つです。
-
勝率は取引回数が増えれば収束するから
-
相場のボラティリティーは日々変化しているから
1つ目の理由は、勝率は取引回数が増えれば増えるほど収束していきますので基準にしやすいという点です。大ざっぱに確認する場合でも取引回数が1000回程度あれば勝率はあらかた収束したと想定する事ができます。
参照記事
確率別の収束速度
二つ目の理由は、相場のボラティリティーは日々変化している為、一律に損切りを100pips、利確を100pipsと固定しても結局は±0の理論確率を超えることはできないと思うからです。相場のボラティリティーに合わせて損切りや利確の値幅を変化させる必要があります。
参照記事
効率的市場仮説の検証
以上の2点の理由から私は勝率を軸にして±0に必要となるレシオを確認した方が良いと判断しています。ちなみに冒頭の式は恒等式ですので、いろいろ変形させることができます。たとえば以下の様な計算式を求めることもできます。
PF1 = ( 1 + レシオ ) × 勝率
※レシオ = 平均利益 ÷ 平均損失 、 PF(プロフィットファクター) = 総利益 ÷ 総損失
恒等式なのでどれか1パターンの計算式を覚えておけばあとは変形させるだけなので便利です。
まとめ
レシオと勝率どちらを軸にするにしても、利益を出すには『レシオに対する±0に必要な勝率』あるいは、『勝率に対する±0に必要なレシオ』を超えなければいけません。
ランダムトレードでは期待値はスプレッド分のマイナスに収束しますので、利益を出すにはランダムトレードでは出来ない何かをする必要があります。
それは待つ事です。
待つにも以下の2種類があります。
-
統計的優位性のあるエントリーポイントまで待つ
-
統計的優位性のあるクローズポイント(決済)まで待つ
結局のところこの2つが利益を出す為の全てです。
統計的優位性があるかどうかはシステムあるいは手法を検証する際、取引回数が1000回以上あり勝率に対する±0に必要なレシオを超えていれば優位性があると判断する事が出来るでしょう。
|
EA名
|
取引回数
|
勝率
|
レシオ
|
±0レシオ
|
差異 ()内%
|
|
リバ取り君
|
1432回
|
67%
|
0.7
|
0.5
|
+0.2(133%)
|
|
伸ばす君
|
2556回
|
28%
|
3.2
|
2.6
|
+0.7(125%)
|
※Lot0.1で2005.2.1~2015.2.1をバックテストした結果
リバ取り君の勝率67%で±0に必要なレシオは0.5です。バックテストの結果0.7という数値を出していますので、エントリーとクローズポイントに優位性があると判断できます。
同様に伸ばす君の勝率28%で±0に必要なレシオは2.6です。バックテストの結果3.2という数値を出していますのでこちらも優位性があると判断できます。
運がいい人の期待値分布
期待値0円のゲームで運よく勝った勝者達だけを集めて再度同じゲームを行った場合、期待値分布はどのようになるのかを検証してみたいと思います。
ゲームのルール
期待値0円のゲームを1000人で実施し、勝った人(0円以上)のみ次のゲームに参加できる。このゲームを4回繰り返し、運がいい人の期待値分布どのようになるのかを確認します。
※勝率50% PF1(SL=100pips TP=100pips) Lot=15万通貨 スプレッド:0
|
ゲーム名
|
参加条件
|
|
テスト1
|
1000人でゲームスタート
|
|
テスト2
|
テスト1で0円以上の利益を出した人のみ参加
|
|
テスト3
|
テスト2で0円以上の利益を出した人のみ参加
|
|
テスト4
|
テスト3で0円以上の利益を出した人のみ参加
|
|
テスト5
|
テスト4で0円以上の利益を出した人のみ参加
|
つまりテスト5に参加できる人はテスト1~4の全ゲームを勝った(0円以上)強運の持ち主という事になります。ゲーム参加人数の推移は以下の様になりました。
1000人でスタートしてテスト5まで残ったのは159人という事が分かりました。はたしてこの強運の持ち主達の期待値分布はどうなっているのでしょうか?
テスト1の期待値分布
まずテスト1の期待値分布がこちらになります。
※試行回数10回を1000人が実施した時の1人当たりの期待値分布
勝率50% PF1(SL=100pips TP=100pips) Lot=15万通貨 スプレッド:0
Lot=15万通貨(固定) 期待値max=+15万 期待値min=-15万 期待値平均=-960円
※縦軸=該当人数 横軸=金額(円)
このゲームの理論期待値は0円です。0円を超える成績を出した人は運が良かったといえますし、0円未満の成績の人は運が悪かったといえます。
ではこのゲームで0円以上の成績を出した運が良い人達だけ(624人)を集めて、再度同じゲームを行った場合(テスト2)期待値分布はどうなるのでしょうか?
テスト2の期待値分布
こちらがテスト2の期待値分布がこちらになります。
※試行回数10回を624人が実施した時の1人当たりの期待値分布
勝率50% PF1(SL=100pips TP=100pips) Lot=15万通貨 スプレッド:0
Lot=15万通貨(固定) 期待値max=+15万 期待値min=-15万 期待値平均=-1797円
※縦軸=該当人数 横軸=金額(円)
赤い線がテスト2の期待値分布です。テスト1で勝った運がいい人達だけを集めてゲームを行ったのですが、結局期待値はテスト1と同じく正規分布している事が分かります。
つまり過去運が良かったからといって将来運が良いとは限らない、またその逆もしかりという事です。
ではさらにテスト2で0円以上の成績を出した運が良い人達だけ(396人)を集めて、再度同じゲームを行った場合(テスト3)期待値分布はどうなるのでしょうか?
テスト3の期待値分布
こちらがテスト3の期待値分布がこちらになります。
※試行回数10回を396人が実施した時の1人当たりの期待値分布
勝率50% PF1(SL=100pips TP=100pips) Lot=15万通貨 スプレッド:0
Lot=15万通貨(固定) 期待値max=+12万 期待値min=-12万 期待値平均=-606円
※縦軸=該当人数 横軸=金額(円)
緑の線がテスト3の期待値分布です。テスト1と2を勝ち残った運がいい人達だけを集めてゲームを行ったのですが、結局期待値はテスト1と同じく正規分布している事が分かります。
では同様にテスト5までの期待値分布を比較してみたいと思います。
テスト1~5の期待値分布比較
※縦軸=該当人数 横軸=金額(円)
結局のところ運がいい人だけ集めたとしても期待値分布が変化する事はありませんでした。これは運の要素からは逃れる事が出来ないという事そして、人間が運をコントロールする事は出来ないという事の証明であります。
まとめ
今回の検証によって以下の2点が分かりました。
-
過去運が良かったからといって将来の運とは無関係である。
-
運は人間にコントロール出来ない
特に運は人間にコントロール出来ないという点についてはしっかりと受け入れる必要があります。運がコントロールできないという事を理解していれば以下の様な言葉に騙される事は無くなるでしょう。
-
貴方は幸せの選択が出来る様になります(あり得ません)
-
運気が上がる方法教えます(あり得ません)
このように運をコントロールしようとすると変な方向へベクトルを向けてしまい、風水・宗教・占い等のオカルトに頼ってしまう恐れがあります。
運というのは人間にはコントロール出来ないと、先人の教えにもこうあります。
人事を尽くして天命を待つ
運という要素が人間にコントロール出来ないからこそ、投資と言うのは難しくも面白くもあるわけです。
では最後に乱数を変化させて期待値分布の変化を確認してみたいと思います。
期待値分布
乱数を変化させても正規分布されていることが確認できます。
分散とヘッジ(相場の世界で信じても良い用語)
相場の世界では覚えても意味の無い用語が多々あります。ボリバン、MACD、RSI、ストキャス、ピボット、フィボナッチ等々覚えても何の役にも立ちません。
しかし信じても良い用語がごく少数あります。そのうちの2つが以下の用語です。
-
分散
-
ヘッジ
分散とヘッジ
相場の世界で信じても良い数少ない用語が、分散とヘッジです。
分散(リスク分散)
ここでいう分散とはリスク分散の事です。リスク分散効果は、相関の無いシステムでポートフォリオを組むことによって得る事が出来るフリーランチの事です。
同じリスク額でもリターンの違うウェイト(組み込み比率)が存在するのはこの事の証明です。
参照記事
ヘッジ(リスクヘッジ)
続いてヘッジですが、ここでいうヘッジとはリスクヘッジの事です。リスクヘッジは主に価格変動リスクを出来るだけ抑えて安定した運用をする為に使います。
FXで平たく言うと両建ての事です。同じタイミングで同じ枚数を両建てすれば価格変動リスクは0になりますが、期待値はスプレッド分のマイナスとなります。
このリスクヘッジというのは金融機関のプロトレーダーであれば必ず行う行為ですし、リスクヘッジせずにポジション持つなんてことは通常ありえない訳です。
なぜならば、市場は概ね効率的ですから将来上がるか下がるかなんて誰にも分からないからです。プロは買ったらあとは上がる様に祈るだけという様な行為はしないと言う事です。
具体的にはプロップトレーダーやファンドマネージャーは、ドル円のコールオプションを買ったら同時にドル円を売ってデルタヘッジします。コールオプションを売ったなら同時にドル円を買ってデルタヘッジします。
同様に日経225のプットオプションを買ったら同時に225先物を買ってデルタヘッジしますし、プットオプションを売ったら同時に225先物を売ってデルタヘッジします。
プロのトレーダーは何にせよ、まずはデルタヘッジして価格変動リスクを無くしたうえでどうやって利益を出していくか戦略を練っていくわけです。
上がるか下がるかは分からなくても今後ボラティリティーが大きくなりそうかどうかはある程度予想できます。ボラが大きくなると予想するのであればリヘッジして利益を出す戦略で行こう!となるわけです。
残念ながら通貨オプション(バニラオプション)を取り扱っているのは国内でサクソバンク証券の1社のみなので、個人が通貨オプションをやるには環境が悪いです。
代わりにバイナリーオプション(BO)などという運の要素しかない期待値マイナスの丁半博打が大流行しているようですが。
という事でドル円等の通貨で気軽にリスクヘッジする場合通常は両建てポジションになるかと思います。
ポートフォリオを組むシステムの相関は本来であれば相関係数を使って分析するべきですが、結構な手間がかかりますので簡単に分析する方法を解説させて頂きます。
それはシステムの勝率と取引回数に着目する方法です。取引回数が多くなれば多くなる程システム本来の勝率に収束していきますので、それを利用するわけです。
勝率が大きく異なればロジックが違うシステムであると推定する事ができます。大ざっぱに確認する場合取引回数が1000回以上あって勝率に大きな差があればOkでしょう。
まとめ
今回分散については主に価格変動に対するリスクの分散について解説しました。価格変動以外でも分散は非常によく使えます。
例えばFX業者によって約定能力も違いますし、スプレッドも違います。1つの業者で運用するより複数の業者で運用した方が、こういったリスクを分散できるといえるでしょう。
私はVPS上で、FXCM・OANDA・外為Finestの3業者で分散運用しています。実際3業者での成績はバラバラです。どこの業者が良いというわけではありません。
分散する事に意義があるのです。