wordpressの更新を長い間していないと発生する。
カテゴリー: お役立ち
光ファイバーはなぜ早いのか
エミュレータ情報
エミュレータ本体情報
https://emu-portal.com/ps.html
使い方
2024年版 PlayStation1 (プレステ1)エミュレータ ePSXe 日本語化・使い方設定方 Windows10/Linux/Mac対応PC
http://emulator.omegumi.com/epsxe_p.html
iso
https://cdromance.com/psx-iso/chocobo-no-fushigi-na-dungeon-jpn/
興味
https://www.su-gaku.net/press_release/detail.php?id=79
知能テスト
https://www.bing.com/search?q=%E3%82%A6%E3%82%A7%E3%82%AF%E3%82%B9%E3%83%A9%E3%83%BC%E5%BC%8F%E7%9F%A5%E8%83%BD%E6%A4%9C%E6%9F%BB+%E5%8F%97%E9%A8%93&qs=n&form=QBRE&sp=-1&pq=%E3%82%A6%E3%82%A7%E3%82%AF%E3%82%B9%E3%83%A9%E3%83%BC%E5%BC%8F%E7%9F%A5%E8%83%BD%E6%A4%9C%E6%9F%BB+%E5%8F%97%E9%A8%93&sc=0-14&sk=&cvid=812D66C2CEFE441BA5C3DBCC8F6929B7
https://adhd-adult.info/hattatsushougai/wais-Ⅲ
https://lscharlie.exblog.jp/24430958/
https://lscharlie.exblog.jp/24428327/
運がいい人の期待値分布
期待値0円ゲームの期待値分布検証
1. ゲームのルール
期待値0円のゲームを1000人で実施し、勝った人(0円以上)のみ次のゲームに参加します。このゲームを4回繰り返し、運がいい人の期待値分布がどのようになるのかを確認します。
ルール概要:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
| ゲーム名 | 参加条件 |
|---|---|
| テスト1 | 1000人でゲームスタート |
| テスト2 | テスト1で0円以上の利益を出した人のみ参加 |
| テスト3 | テスト2で0円以上の利益を出した人のみ参加 |
| テスト4 | テスト3で0円以上の利益を出した人のみ参加 |
| テスト5 | テスト4で0円以上の利益を出した人のみ参加 |
2. テスト1の期待値分布
テスト1の期待値分布は以下の通りです。試行回数10回を1000人が実施した際の1人当たりの期待値分布です。
条件:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
Lot=15万通貨(固定)、期待値max=+15万、期待値min=-15万、期待値平均=-960円
3. テスト2の期待値分布
テスト1で運が良かった人(624人)のみを集めて再度ゲームを行った結果の期待値分布です。
条件:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
Lot=15万通貨(固定)、期待値max=+15万、期待値min=-15万、期待値平均=-1797円
4. テスト3の期待値分布
テスト2で運が良かった人(396人)のみを集めて再度ゲームを行った結果の期待値分布です。
条件:勝率50%、PF1(SL=100pips、TP=100pips)、Lot=15万通貨、スプレッド:0
Lot=15万通貨(固定)、期待値max=+12万、期待値min=-12万、期待値平均=-606円
5. テスト1~5の期待値分布比較
テスト1からテスト5まで、運が良かった人だけを集めてゲームを続けた結果、期待値分布に変化は見られませんでした。運の要素からは逃れることができないという事実が確認できました。
6. まとめ
今回の検証で以下のことが分かりました:
- 過去運が良かったからといって将来も運が良いとは限らない。
- 運は人間にコントロールできない。
「人事を尽くして天命を待つ」という言葉が示すように、運という要素が人間にコントロールできないからこそ、投資は難しくもあり、また面白いのです。
分散とヘッジ
分散とヘッジ: 相場の世界で信じられる数少ない用語
1. 分散とヘッジとは
相場の世界では、多くの専門用語が飛び交っていますが、その中には学んでも実践的な意味を持たないものもあります。例えば、ボリバン、MACD、RSIなどです。しかし、数少ない信じるに足る用語として「分散」と「ヘッジ」が挙げられます。
2. 分散 (リスク分散)
分散とはリスク分散を指します。リスク分散効果は、相関のないシステムを組み合わせてポートフォリオを構築することで得られる「フリーランチ」のようなものです。同じリスク額でも、リターンが異なるウェイト(組み込み比率)が存在することがこの理論を裏付けています。
例えば、複数の業者で取引を分散させることで、約定能力やスプレッドの違いから生じるリスクを軽減することが可能です。
3. ヘッジ (リスクヘッジ)
ヘッジとは、価格変動リスクを抑えるための手法を指します。例えば、FX取引における両建てがこれに該当します。同じタイミングで同じ枚数を両建てすれば、価格変動リスクはゼロになりますが、期待値はスプレッド分だけマイナスとなります。
金融機関のプロトレーダーであれば、リスクヘッジをせずにポジションを持つことは通常あり得ません。市場は概ね効率的であり、将来の価格変動を正確に予測することは不可能だからです。
4. システム相関の簡易分析
ポートフォリオを組む際、本来は相関係数を使った詳細な分析が求められますが、これは手間がかかります。そのため、より簡単な方法として「システムの勝率」と「取引回数」に着目する方法があります。
取引回数が多くなればなるほど、システム本来の勝率に収束していきます。この特性を利用することで、異なるロジックを持つシステムを大まかに判断することが可能です。例えば、取引回数が1000回以上あり、勝率に大きな差がある場合、それぞれのシステムは異なるロジックに基づいていると推測できます。
5. まとめ
分散とヘッジは、相場の世界で信頼できる数少ない用語です。これらを活用することで、リスクを軽減し、より安定した取引を目指すことが可能となります。特に、リスクを分散させることで、複数のシステムや業者を活用する意義が強調されます。
分散することには意義があります。複数の要素を組み合わせてリスクを軽減し、より効果的なトレードを目指しましょう。
パチンコの勝ち方_確率的視点
1. パチンコは勝てるのか?
パチンコで稼いでいる(食っている)人は、確率を理解し、勝つべくして勝っています。
パチンコで勝てる理由
パチンコで勝っている人(パチプロ)は、偶然勝っているのではなく、
確率と期待値を理解しているのです。
まず断っておきたいのですが、投資系の話をする人でパチンコは勝てないなどと言ってる人は論外なのでそういう人の話は聞き流した方が身のためです。
パチンコで勝っている人(パチプロ)は運よく偶然勝っているのではなく、確率と期待値の事を理解し勝つべくして勝っているのです。
不思議な事に、学者の先生や高学歴の秀才達ほどパチンコは勝てないとはなから思い込んでいる方が多い様に思います。
当然、数学者の先生方は数学に関して誰よりも博識であるのは明白なのですが、なぜがパチンコなんて勝てるわけないとおっしゃいます。
私見ですがおそらく、学者の先生や高学歴の秀才達はおそらく人生でパチンコなどという低俗なものと関わることなく人生を歩んでこられたのではないかと思います。
だから確率や数学又は統計の知識に関しては誰よりも博識であるにもかかわらず、パチンコは勝てないとはなから思い込んでいるものと推定されます。
たしかにパチンコは低俗なマネーゲームです。そこは認めましょう。しかしながら、パチンコで勝てないという点に関してはただの思い込みであると反論させて頂きます。
パチンコで勝てない要因
- パチンコなどという低俗なものに関わり合いたくない
- 確率を理解していない
- 確率を理解しているが実行できていない
パチンコで勝てない要因を大きく分けると上記の3つになるかと思います。
まず1つ目のパチンコに関わり合いたくないという方は、勝ちようがありません。先述しましたが、学者の先生や高学歴の秀才に多くみられる傾向にあります。これはもうしょうがないです。確かにパチンコなどと言う低俗なものに関わり合いたくない気持ちもよく分かりますので。
続いて2番目の確率の事を理解していないに当てはまる方は、確率の事を理解すれば勝てる様になる可能性があります。あくまで可能性ですけど。
そして一番多いのが3番目の確率の事を理解しているけれども実行できていない方です。ここに当てはまる方がパチンコで勝てない人の大多数を占めています。
よくあるのがボーダーを知っているのに勝てないという方です。これはパチンコの事を分かったつもりになっているだけで、パチンコというゲームの本質を理解していない事の現れです。
ちなみにパチプロでボーダーがいくらか重要視している人はまずいません。ボーダーなど知っているのは当たり前だし、それだけで食えるような甘い世界では無いからこそ、その他の部分で色々な技術介入をしているわけです。
1000円当たり22回回った!これは期待値プラスの台だ!と喜んで打ってる人はパチンコというゲームの本質を理解している気になっているだけのにわかです。いわゆる初心者ってやつです。そしてその初心者が大半をしめているのがパチンコというマネーゲームの世界です。
パチンコというマネーゲームはパチンコ屋の経費(電気代や人件費等)を引くと完全にマイナスサムゲームの世界です。一般的にパチンコの還元率は85%と言われています。
つまりパチンコというマネーゲームに参加した人全員から集めたお金の85%をプレイヤーで奪い合うマネーゲームであるという事をまず理解する必要があります。
という事でパチンコで実際食えるほど稼いでる人というのは優良店当たり数人程度でしょう。その数人がパチンコというマネーゲームでの数少ない本物の勝者という事になります。
パチンコで勝つのに難しい数式を覚える必要はありません。確率の収束と大数の法則だけ理解していれば十分です。
下記が当選確率1/100(理論値)のパチンコ台の当選確率と回転数の関係を表したものになります。
パチンコというマネーゲームの本質
パチンコはマイナスサムゲームであり、還元率は約85%とされています。
パチプロが勝つには、期待値を積み上げる戦略が必要です。
期待値の仕組み
回転数4000回を超えたあたりから理論確率(1/100)付近に収束している事が分かります。ちなみに、パチプロが一日ぶん回して2000回転程度ですので、4000回転は2日間フル稼働したものだと思って頂けたら宜しいかと思います。
つまり、1日フル稼働しただけでは理論確率に収束しきれないという事が分かります。ましてや会社帰りに数時間稼働しただけでは理論確率に収束するのはいつになるのやらという事が分かります。
理論確率より多く当たれば、運が良いといいますし、少なければ運が悪いといいます。確率が収束していない段階(回転数が少ない段階)の当選確率というのは運が支配している事も理解頂けるかと思います。
では実際パチンコでどうやって勝つの?
回転数を増やせば増やすほど理論確率(今回の場合1/100)に近づくという事は、どうすれば利益を出す事が出来るか考えてみて下さい。
ヒントはシステムトレードにおけるPF(プロフィットファクター)です。PFとは総利益÷総損失で表される数字です。
例えば勝率50%のシステムが利益を出すには、総損失が100万円とすると、それを超える総利益(100万円超え)を出す必要があります。つまり勝率50%の場合リスクリワードが1を超えないと利益が出ないという事です。
パチンコも一緒です。今回の場合最終的に1/100の確率に収束するという事は、100回転させるのに使った金額(総損失)より、当選した時にもらえる金額(総利益)の方が多ければ期待値はプラスであり、回せば回すほど期待値が積み上げられていきます。
とどのつまりパチンコで勝つというのはそういう事なのです。
あとはそれを実行できるか?
パチンコでは期待値を積み重ねていっても運の要素(偶然)によって実収支がマイナスになる事はよくあります。具体的には期待値100万稼いだけど実収支は50万しかなかったという事は多々あります。
さらに短いスパンの場合、例えば一日単位で見てみてみますと、期待値+3万出したけど実収支は-7万だったという事も多々あります。
この期待値と実収支の乖離は完全に運(偶然)です。むろんプラス側に行く時もあります。この様に偶然というのは避けることの出来ない普遍的な事だという事を理解する必要があります。
偶然のブレ(主に下振れ収支)が起こったとしても心を乱すことなく、ただ淡々と期待値を追いかけることが出来る人がパチプロという数%しかいないパチンコ界におけるマネーゲームの勝者なのです。
今年は期待値まで100万足りてないっ!って笑って話せるような人が確率の事を本当に理解し、実際行動に移すことが出来ている本物のパチプロと呼ばれる方々です。
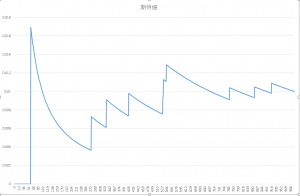
当選確率と回転数の関係
パチンコで勝つ方法
パチンコで勝つには、期待値を理解し、実行することが求められます。以下のポイントを考慮しましょう:
- 期待値がプラスの台を選ぶ。
- 確率の収束と大数の法則を理解する。
- 短期的な収支のブレに動じない。
期待値と実収支の乖離
期待値を積み重ねても、短期的な実収支はブレる可能性があります。これを理解し、冷静に行動できる人が本物のパチプロです。
まとめ
パチンコで勝つには確率を理解し、期待値を積み上げることが重要です。短期的な運に左右される場面があっても、確率の本質に基づき行動することで、勝利を収めることが可能です。
期待値と確立
確率別の収束速度について
今回は確率別の収束速度について解説させて頂きます。
目次
1. コインゲームの期待値
まずは直感でも分かり易い、コインゲームの期待値を考えてみたいと思います。
★コインゲームのルール
表が出たら200円貰える
裏が出たら100円支払う
このコインゲームの1プレイ当たりの期待値は幾らでしょうか?
答えは:
期待値= ( 1/2 × -100円 + 1/2 × +200円 ) × 1回 = +50円
2. サイコロゲームの期待値
次に、サイコロゲームの期待値を考えてみたいと思います。
★サイコロゲームのルール
1が出たら800円貰える
1以外が出たら100円支払う
答えは:
期待値= ( 5/6 × -100円 + 1/6 × +800円 ) × 1回 = +50円
3. ゲームに参加するべきか?
両ゲームとも1プレイ当たりの期待値はプラスですが、プレイ回数が重要です。最低でも200回以上プレイできる条件で参加するべきです。
なぜなら、試行回数が少ない内は運の要素が強く、理論値に収束しにくいためです。
4. 確率の収束と大数の法則
試行回数が増えるほど、理論値に収束する傾向があります。この現象を大数の法則と呼びます。
以下は勝率20%、40%、60%のシステムにおける試行回数と確率の収束を示すグラフです:

5. コインゲームとサイコロゲームのまとめ
1プレイ当たりの期待値がプラスで、かつ200回以上プレイできる条件を満たした場合のみ参加するべきです。
試行回数が少ない場合、偶然が収益に大きく影響を与えることを理解しましょう。
6. システムトレードにおける試行回数
取引回数が多いほどシステムの勝率は本来の値に収束します。200回未満のバックテスト結果は信頼性が低い可能性が高いです。
確率別の収束速度
1. ゲームのルール
今回は確率別の収束速度について解説させて頂きます。
2. コインゲームの期待値
まずは直感でも分かり易い、コインゲームの期待値を考えてみたいと思います。
★コインゲームのルール
表が出たら200円貰える
裏が出たら100円支払う
このコインゲームの1プレイ当たりの期待値は幾らでしょうか?
答えは、
期待値= ( 1/2 × -100円 + 1/2 × +200円 ) × 1回 = +50円 となります。
3. サイコロゲームの期待値
では次に、サイコロゲームの期待値を考えてみたいと思います。
★サイコロゲームのルール(※6面体のサイコロ)
1が出たら800円貰える
1以外が出たら100円支払う
このサイコロゲームの1プレイ当たりの期待値は幾らでしょうか?
答えは、
期待値= ( 5/6 × -100円 + 1/6 × +800円 ) × 1回 = +50円 となります。
4. ゲームに参加するべきか?
では、この期待値が+50円のコインゲーム又はサイコロゲームに参加するべきでしょうか?
答えは、プレイできる回数によるが正解となります。
両ゲームとも1プレイ当たりの期待値はプラスですが、プレイできる回数が例えば10回だけと決まっているのであれば参加するべきではありません。
5. 確率の収束と大数の法則
それでは実際、どの様に確率が収束していくのかをグラフで見てみましょう。
エクセルで勝率20%・40%・60%のシステムを作成し、各システムの勝率と試行回数の関係をグラフにして表したものがこちらです。(試行回数1,000回を実施)
6. まとめ
ゲームに参加するべきかどうかの判断は、まずそのゲームの1回当たりの期待値がプラスである事、そしてそのゲームを最低でも200プレイできる事、という2つの条件をクリアした場合のみ参加すれば良いという結論になります。
この様に確率というのは試行回数が少ないうちは偶然(運)が支配するものであることをご理解頂けたかと思います。
