投稿者: mikazuki

bashデバック

参照:http://shellscript.sunone.me/debug.html

JSP＊タグリファレンス

http://tag.main.jp/index.html

システムモニタリングコマンド一覧

最近SQL・データベースを扱うことが多いのですが、その際に手放すことができないレベルの超便利ツールのSQL実行ツールであるA5:SQL Mk-2というのがあります。 そのA5:SQL Mk-2の便利なショートカットをまとめてみました。 Ctrl + q SQL整形 Ctrl + g 条件を指定してテーブルを開く Ctr…

情報源: 便利ツール　A5:SQL Mk-2の便利なショートカットをまとめてみた – 思考停止するな

ダミーデータ作成

https://a5m2.mmatsubara.com/help/TableEditor/dummy.html

・基本情報
http://www.techscore.com/tech/Java/ApacheJakarta/JMeter/index/

・統計レポートの見方
https://e-algorithm.xyz/jmeter/#jump4

・apache-jmeter-3.3\bin\jmeter-server.bat
に以下の設定を入れる

:port
call jmeter -Dserver_port=%SERVER_PORT% -s -j jmeter-server.log %JMETER_CMD_LINE_ARGS% 【-Dsun.net.inetaddr.ttl=0 -Dsun.net.inetaddr.negative.ttl=0】

詳細は
https://qiita.com/arai-wa/items/492d91d85a7473007e37

・実行bat sample
set time2=%time: =0%
set PREFIX=%date:~-10,4%%date:~-5,2%%date:~-2,2%%time2:~0,2%%time2:~3,2%%time2:~6,2%
cmd /k jmeter.bat -n -t .\FINAL\LJ53.jmx -j .\FINAL\result\%PREFIX%_jmeter.log -l .\FINAL\result\%PREFIX%_result.jtl

詳細は
https://qiita.com/tatesuke/items/827e6190753964e46814

windowsパフォーマンスモニター
http://www.atmarkit.co.jp/ait/articles/0910/30/news114.html

情報源: 統計的検定の考え方 – 大人になってからの再学習

パチンコは勝てるのか？

パチンコで稼いでる(食っている)人というのは確率の事を理解して勝つべくして勝っています。

まず断っておきたいのですが、投資系の話をする人でパチンコは勝てないなどと言ってる人は論外なのでそういう人の話は聞き流した方が身のためです。

パチンコで勝っている人(パチプロ)は運よく偶然勝っているのではなく、確率と期待値の事を理解し勝つべくして勝っているのです。

不思議な事に、学者の先生や高学歴の秀才達ほどパチンコは勝てないとはなから思い込んでいる方が多い様に思います。

当然、数学者の先生方は数学に関して誰よりも博識であるのは明白なのですが、なぜがパチンコなんて勝てるわけないとおっしゃいます。

私見ですがおそらく、学者の先生や高学歴の秀才達はおそらく人生でパチンコなどという低俗なものと関わることなく人生を歩んでこられたのではないかと思います。

だから確率や数学又は統計の知識に関しては誰よりも博識であるにもかかわらず、パチンコは勝てないとはなから思い込んでいるものと推定されます。

たしかにパチンコは低俗なマネーゲームです。そこは認めましょう。しかしながら、パチンコで勝てないという点に関してはただの思い込みであると反論させて頂きます。
パチンコで勝てない要因３つ

パチンコなどという低俗なものに関わり合いたくない
確率の事を理解していない
確率の事を理解しているけれども実行できていない

パチンコで勝てない要因を大きく分けると上記の３つになるかと思います。

まず１つ目のパチンコに関わり合いたくないという方は、勝ちようがありません。先述しましたが、学者の先生や高学歴の秀才に多くみられる傾向にあります。これはもうしょうがないです。確かにパチンコなどと言う低俗なものに関わり合いたくない気持ちもよく分かりますので。

続いて２番目の確率の事を理解していないに当てはまる方は、確率の事を理解すれば勝てる様になる可能性があります。あくまで可能性ですけど。

そして一番多いのが３番目の確率の事を理解しているけれども実行できていない方です。ここに当てはまる方がパチンコで勝てない人の大多数を占めています。

よくあるのがボーダーを知っているのに勝てないという方です。これはパチンコの事を分かったつもりになっているだけで、パチンコというゲームの本質を理解していない事の現れです。

ちなみにパチプロでボーダーがいくらか重要視している人はまずいません。ボーダーなど知っているのは当たり前だし、それだけで食えるような甘い世界では無いからこそ、その他の部分で色々な技術介入をしているわけです。

1000円当たり22回回った！これは期待値プラスの台だ！と喜んで打ってる人はパチンコというゲームの本質を理解している気になっているだけのにわかです。いわゆる初心者ってやつです。そしてその初心者が大半をしめているのがパチンコというマネーゲームの世界です。

パチンコというマネーゲームはパチンコ屋の経費(電気代や人件費等)を引くと完全にマイナスサムゲームの世界です。一般的にパチンコの還元率は85%と言われています。

つまりパチンコというマネーゲームに参加した人全員から集めたお金の85%をプレイヤーで奪い合うマネーゲームであるという事をまず理解する必要があります。

という事でパチンコで実際食えるほど稼いでる人というのは優良店当たり数人程度でしょう。その数人がパチンコというマネーゲームでの数少ない本物の勝者という事になります。

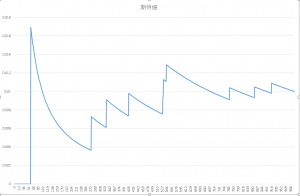
パチンコで勝つのに難しい数式を覚える必要はありません。確率の収束と大数の法則だけ理解していれば十分です。

下記が当選確率1/100(理論値)のパチンコ台の当選確率と回転数の関係を表したものになります。

回転数4000回を超えたあたりから理論確率(1/100)付近に収束している事が分かります。ちなみに、パチプロが一日ぶん回して2000回転程度ですので、4000回転は2日間フル稼働したものだと思って頂けたら宜しいかと思います。

つまり、1日フル稼働しただけでは理論確率に収束しきれないという事が分かります。ましてや会社帰りに数時間稼働しただけでは理論確率に収束するのはいつになるのやらという事が分かります。

理論確率より多く当たれば、運が良いといいますし、少なければ運が悪いといいます。確率が収束していない段階(回転数が少ない段階)の当選確率というのは運が支配している事も理解頂けるかと思います。

では実際パチンコでどうやって勝つの？

冒頭で申しました通り、現役で稼いでる方の迷惑にならない範囲でお答えさせて頂きます。

回転数を増やせば増やすほど理論確率(今回の場合1/100)に近づくという事は、どうすれば利益を出す事が出来るか考えてみて下さい。

ヒントはシステムトレードにおけるPF(プロフィットファクター)です。PFとは総利益÷総損失で表される数字です。

例えば勝率50%のシステムが利益を出すには、総損失が100万円とすると、それを超える総利益(100万円超え)を出す必要があります。つまり勝率50%の場合リスクリワードが1を超えないと利益が出ないという事です。

パチンコも一緒です。今回の場合最終的に1/100の確率に収束するという事は、100回転させるのに使った金額(総損失)より、当選した時にもらえる金額(総利益)の方が多ければ期待値はプラスであり、回せば回すほど期待値が積み上げられていきます。

これ以上は現役の方の迷惑になる可能性が高いので言えませんが、とどのつまりパチンコで勝つというのはそういう事なのです。
あとはそれを実行できるか？

パチンコでは期待値を積み重ねていっても運の要素(偶然)によって実収支がマイナスになる事はよくあります。具体的には期待値100万稼いだけど実収支は50万しかなかったという事は多々あります。

さらに短いスパンの場合、例えば一日単位で見てみてみますと、期待値+3万出したけど実収支は-7万だったという事も多々あります。

この期待値と実収支の乖離は完全に運(偶然)です。むろんプラス側に行く時もあります。この様に偶然というのは避けることの出来ない普遍的な事だという事を理解する必要があります。

偶然のブレ(主に下振れ収支)が起こったとしても心を乱すことなく、ただ淡々と期待値を追いかけることが出来る人がパチプロという数%しかいないパチンコ界におけるマネーゲームの勝者なのです。

今年は期待値まで100万足りてないっ！って笑って話せるような人が確率の事を本当に理解し、実際行動に移すことが出来ている本物のパチプロと呼ばれる方々です。

今回はシステムの勝率別に起こりうる最大連敗数を求めてみたいと思います。

N回連続して負ける確率
勝率x%のシステムがN回連続して負ける確率は以下の様に求めることが出来ます。

N回連続して負ける確率 = ( 1 – 勝率x )＾N回

この式を使って、勝率50%のシステムが5回連続して負ける確率を求めてみますと、
■5連敗する確率 ＝ ( 1 – 50% )＾5回　=　3.1% 　となります。

では10回連続して負ける確率も求めてみますと
■10回連敗する確率 ＝ ( 1 – 50% )＾10回　=　0.1% 　となります。

以上の事から勝率50%のシステムにおいては、5連敗する確率が3.1%で、10連敗する確率が0.1%という事が分かりました。

それでは今度は勝率x%のシステムにおいて、1%の確率で起こりうる連敗数Nを求めてみたいと思います。

起こりうる連敗数N
冒頭の計算式を展開して、N連敗する確率に1%を代入しますと以下の様になります

N連敗する確率 = ( 1 – 勝率x )＾N回
連敗数N = LOG₍₁₋ₓ₎1%　この式をエクセルのLOG関数を使うと以下の様になります。
※スマホでご覧の方へ⇒LOGの底に(1-x)と記載しております。

連敗数N = LOG( 1% , 1-勝率x )

この式から勝率50%のシステムにおいて1%の確率で起こりうる連敗数Nは、
■連敗数N = LOG ( 1% , 1-50% )　=　6.6回　となります。

以上の事から勝率50%のシステムにおいては最大6.6連敗する可能性が1%あるという事が分かりました。

1%の部分を危険率α(計算を間違える確率)と置き換えますと、最終的に以下の式になります。

連敗数N = LOG( 危険率α , 1-勝率x )

この計算式により、危険率αの場合に勝率x%のシステムで起こりうる連敗数Nを求める事が出来ます。

エクセルのLOG関数について
エクセルのLOG関数は、”=LOG(真数,底)”と入力するとその対数を返します。
対数とは、底を何乗したら真数になるかを表すものです。

ex.1　LOG₂4　=　LOG(4,2)　=　2　※2(底)を2乗したら4(真数)になる。
ex.2　LOG₂256　=　LOG(256,2)　=　8　※2(底)を8乗したら256(真数)になる。

勝率別に起こりうる最大連敗数一覧
以下の表がシステムの勝率別に起こりうる最大連敗数の一覧になります。
危険率1%と0.0001%の2パターンを求めています。

小数点は四捨五入、α=危険率、0.0001%=1ppm(100万分の1)

注意点(勝率の収束)
システムの勝率から最大連敗数を予測する上で非常に重要となるのが、そのシステムの勝率が収束しているかどうかです。取引回数が200回に満たない場合の勝率というのはシステム本来の勝率に収束していない可能性が高いので注意が必要です。

詳しくは下記記事の”確率の収束と大数の法則”をご参照下さい。

連敗数を予想してトレードにどう生かすか？
自分の運用しているシステムの勝率を確認して、最大何連敗する可能性があるのか理解する事によって、実際連敗が起こった時にパニックになって稼働を停止してしまわない様に心の準備ができます。

勝率が80%のシステムでも絶望的に運が悪ければ9連敗する事もありえるという事を知識として知っていれば、心を乱すことなくトレードを継続できます。

今回は確率別の収束速度について解説させて頂きます。大数の法則によって確率は収束しますが、確率によって収束するスピードは異なるはずです。

つまり確率1/2(50%)と1/100(1%)とでは収束するのに必要な試行回数(収束速度)が違うという事です。大数の法則の詳細についてはこちらのブログを検索してください。

確率が収束するのに必要となる試行回数nを求める

確率分母kが誤差±r%以内に収束するのに必要となる試行回数n(危険率5%)は以下の計算式で求めることが出来ます。

n=試行回数　z=(今回は危険率5%で1.96)　k=確率分母　r=誤差
※危険率=計算を間違える確率

試行回数n = 1.96^2 × ( 確率分母k – 1 ) ÷ 誤差r^2

この計算式を使って、勝率50%(確率分母2)システムの勝率が誤差±10%以内に収束するのに必要となる試行回数nを求めてみますと、
■n = 1.96^2 × ( 2 – 1 ) ÷ 10%^2 = 384回　となります。

以上の事から、勝率50%システムの勝率が誤差±10%以内(45~55%)に収束するのには、95％の確率で試行回数が384回以上必要という事が分かりました。

※なぜこの計算式になるのかはこちらのサイト様が解説して下さっています。
http://www.dwdem.com/math/lec/page21_1.html

・確率別の収束速度一覧

以下の表が確率別の収束に必要となる試行回数の一覧となります。危険率は5%で、誤差は±10%で求めています。

確率が低くなればなるほど、収束するのに必要となる試行回数が増えていっているのが分かります。勝率30%のシステムが誤差±10%の確率に収束するには95%の確率で取引回数896回以上が必要となる事が分かります。

つまり取引回数が896回未満で勝率が30%のバックテスト結果があったとしても、その成績はまだシステム本来の勝率に収束していない、あてにならない成績である確率が高い事が分かります。

ribadorikun　総取引回数：1,432回　PF：1.33　勝率67%
nobasukun　総取引回数：2,556回　PF：1.26　勝率28%

バックテストの成績を見る際は、取引回数と勝率をチェックして、システム本来の勝率に収束しているかを確認する事がきわめて重要となります。

ではエクセルで上記表の勝率となるシステムを作成し、確率の収束具合を目視で確認してみたいと思います。

試行回数1000回を超えればどの勝率のシステムでも大方確率が収束している事が分かります。
おおざっぱに見ても1000回程度を超えればあらかた確率が収束している様にも見えます。

・低確率の場合の収束速度一覧

システムトレードでの勝率は低くても20%(1/5)程度ですが、たとえばパチンコの様な低確率の場合収束するのに必要となる試行回数がどうなるかを表したのが以下の表です。危険率は5%で、誤差は±10%で求めています。

パチンコの当選確率が1/100だった場合、38,030回転以上させないと誤差±10%以内の確率(1/91 ~ 1/111)に収束しない事が分かります。パチプロは1日2000回転させますので、約20日分です。つまりパチプロが1か月フル稼働させてやっと誤差±10%以内の確率に収束するという事が分かります。

パチンコの勝ち方についてはこちらのブログを検索してください。

この様に大数の法則によって確率は収束するのですが、確率が低ければ低い程収束するのに必要な試行回数が増えていくことが分かりました。テスターレポートをおおざっぱに確認する場合、バックテストの取引回数が1000回以上あり優秀な成績を出しているシステムであれば一安心でしょう。

FX 実戦チャート術 第11回 ダウ理論&RCI｜FX｜外為オンライン　FX取引 － あなたの為の、外為を。.